- Avtor Matthew Elmers [email protected].
- Public 2023-12-16 22:33.
- Nazadnje spremenjeno 2025-01-24 09:35.

Kaj določa natančnost - eno glavnih značilnosti orožja? Očitno iz kakovosti cevi in kartuše. Odložimo kartušo za zdaj, vendar razmislimo o fiziki postopka.
Vzemite kovinsko palico ali cev iz elastične kovine in jo trdno pritrdite v masivno podlago. Tako dobimo model proučevane naprave. Zdaj, če udarimo v palico, ni pomembno, na katerem mestu in v katero smer, ali jo potegnemo nazaj ali stisnemo, ali na koncu vstavimo kartušo v cev in izstrelimo strel, bomo videli, da palica (sod) prišel v blaženo nihajno gibanje. Te vibracije se razgradijo v najpreprostejše in vsaka vrsta tako preprostega tresljaja cevi bo na svoj način vplivala na natančnost (natančnost) streljanja.
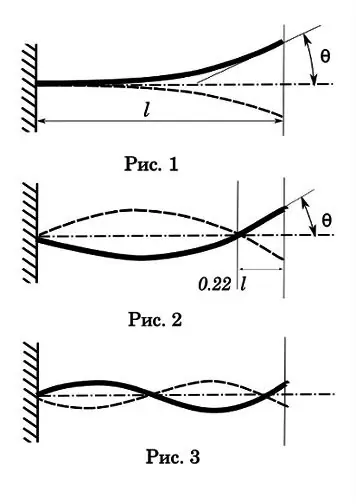
Začnimo z vibracijami prvega reda ali višine. Kot lahko vidite (slika 1), ima tako nihanje le eno vozlišče na mestu pritrditve, največjo amplitudo, najdaljši čas razpada in najdaljši čas nihanja enega obdobja. Ta čas je 0,017-0,033 sek. Čas potovanja krogle skozi izvrtino je 0, 001-0, 002 sek. To je bistveno manj kot cikel enega nihanja, kar pomeni, da tovrstno nihanje nima pomembnega vpliva na natančnost enega posnetka. Toda s samodejnim snemanjem se lahko izkaže zanimiva slika. Recimo, da je hitrost ognja 1200 vrt / min, tj. čas enega cikla - 0,05 sek. Z obdobjem nihanja prvega reda 0, 025 sekund imamo razmerje več frekvenc. In to je nepogrešljiv pogoj za resonanco z vsemi posledičnimi posledicami - orožje se začne tresti s takšno silo, da lahko razpade.
Preidimo na nihanja drugega reda (slika 2). Predlagam pa, da študentje humanistike najprej izvedejo poskus, da bi odpravili pomanjkljivosti izobraževanja na področju fizike. Morate vzeti dečka (lahko dekle), ga postaviti na gugalnico in zanihati. Pred vami je nihalo. Stojte na strani gugalnice in dečka poskusite udariti z žogo. Po vrsti poskusov boste prišli do zaključka, da je najboljši način zadetka, ko je tarča v prvi fazi nihanja - največje odstopanje od točke ravnotežja. Na tej točki ima cilj ničelno hitrost.
Poglejmo diagram drugega reda. Drugo vozlišče vibracij se nahaja približno 0,22 od konca cevi. Ta točka je naravni zakon, za konzolni žarek je nemogoče ustvariti takšne vibracije, tako da drugo vozlišče pade na prosti konec. Tam je in ni odvisno od dolžine cevi.
Amplituda nihanja za shemo drugega reda je nižja, vendar je čas nihanja že primerljiv s časom prehoda krogle skozi izvrtino-0, 0025-0, 005 sek. Torej za posamično streljanje je to že zanimivo. Da bi bilo jasno, o čem govorimo, si predstavljajte sod, dolg 1 meter. Krogla potuje skozi celotno cev v 0,001 sekundah. Če je obdobje nihanja 0,004 sekunde, bo do trenutka, ko krogla zapusti cev, cev v prvi fazi dosegla največji upogib. Vprašanje za humanistiko je, v katerem trenutku (v kateri fazi) je najbolje izstreliti kroglo iz cevi, da se zagotovi doslednost rezultatov? Spomnite se zamaha. Na ničelni točki je vektor hitrosti odklona debla največji. Krogla težje zadene to točko na prerezu cevi, ima tudi svojo napako pri hitrosti. To pomeni, da bo najboljši trenutek, da bo krogla izletela, ko bo cev na najvišji točki prve odklonske faze - kot na sliki. Potem se bodo neznatna odstopanja v hitrosti krogle izravnala z daljšim časom, ki ga cev preživi v svoji najbolj stabilni fazi.
Grafični prikaz tega pojava je jasno razviden iz diagrama (slika 4-5). Tu je Δt časovna napaka, s katero krogla prečka gobec cevi. Na sl. 4 je idealno, če povprečni vzlet krogle sovpada z ničelno fazo nihanja cevi. (Matematiki! Vem, da je porazdelitev hitrosti nelinearna.) Zasenčeno območje je kot širjenja poti.
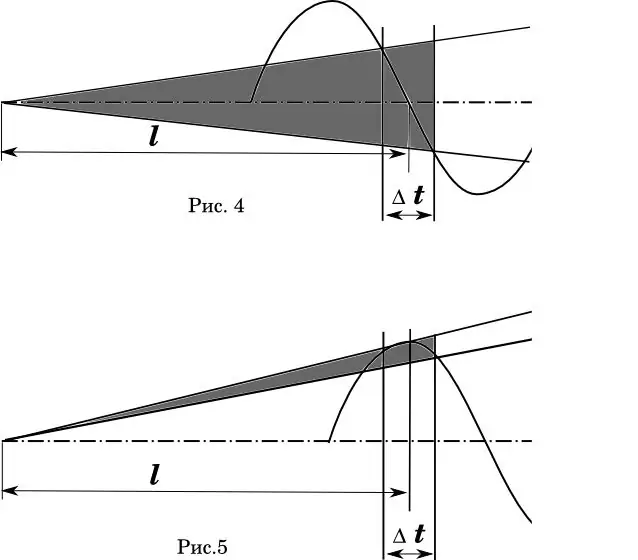
Na sliki 5 dolžina cevi in hitrostna napaka ostajata enaka. Toda faza upogibanja cevi se premakne tako, da povprečni čas odhoda sovpada z največjim odklonom cevi. So komentarji odveč?
No, je vredno sveče? Kako resna so lahko odstopanja, ki jih povzročajo nihanja drugega reda? Resno in zelo resno. Po mnenju sovjetskega profesorja Dmitrija Aleksandroviča Ventzela so v enem od poskusov dobili naslednje rezultate: polmer sredinskega odstopanja se je s spremembo dolžine cevi povečal le za 100 mm. Za primerjavo: kakovostna obdelava cevi lahko izboljša natančnost le za 20%!
Zdaj pa poglejmo formulo za frekvenco vibracij:
kje:
k - koeficient za nihanja drugega reda - 4, 7;
L je dolžina cevi;
E je modul elastičnosti;
I je vztrajnostni moment odseka;
m je masa debla.
… in nadaljujte z analizo in zaključki.
Očiten zaključek iz slik 4-5 je napaka hitrosti krogle. Odvisno je od kakovosti prahu ter njegove teže in gostote v vložku. Če je ta napaka vsaj četrtina časa cikla, se lahko vsemu drugemu odrečemo. Na srečo sta znanost in industrija v tej zadevi dosegli zelo veliko stabilnost. Za bolj izpopolnjene (na primer v klopci) obstajajo vsi pogoji za samosestavljanje kartuš, da se faza sproščanja krogle prilagodi natančno dolžini cevi.
Torej imamo kartušo z najmanjšo možno variacijo hitrosti. Dolžina cevi je bila izračunana na podlagi njene največje teže. Postavlja se vprašanje stabilnosti. Pogledamo formulo. Katere spremenljivke vplivajo na spremembo frekvence nihanja? Dolžina cevi, modul elastičnosti in masa. Cev se med streljanjem segreje. Lahko toplotno spremeni dolžino cevi, kar vpliva na natančnost. Da in ne. Da, ker ta številka leži pri stotinah odstotka pri temperaturi 200 C. Ne, ker je sprememba modula elastičnosti jekla za isto temperaturo približno 8-9%, je pri 600C skoraj dvakrat. Se pravi, večkrat višje! Cev postane mehkejša, faza upogibanja cevi se premakne naprej za trenutek, ko krogla zapusti, natančnost pade. No, kaj pravi premišljen analitik? Rekel bo, da je nemogoče doseči največjo natančnost na eni dolžini cevi v hladnem in vročem načinu! Orožje je lahko boljše pri hladnem ali vročem ceveh. V skladu s tem dobimo dva razreda orožja. Eden je za dejanja iz zasede, ko je treba tarčo zadeti iz prvega - "hladnega" strela, ker bo natančnost drugega slabša zaradi neizogibnega segrevanja cevi. V takem orožju ni nujne avtomatizacije. In drugi razred so avtomatske puške, katerih dolžina cevi je prilagojena vroči cevi. V tem primeru je možno zgrešitev zaradi nizke natančnosti hladnega strela mogoče nadomestiti s hitrim poznejšim vročim in natančnejšim strelom.
EF Dragunov je zelo dobro poznal fiziko tega procesa, ko je oblikoval svojo puško. Predlagam, da se seznanite z zgodbo njegovega sina Alekseja. Najprej pa si bo moral nekdo zlomiti možgane. Kot veste, sta se dva vzorca Konstantinova in Dragunova približala finalu tekmovanja za ostrostrelsko puško. Oblikovalci so bili prijatelji in si pri vsem pomagali. Tako je bila puška Konstantinova "nastavljena" na hladen način, puška Dragunova pa na "vroča". V poskusu izboljšanja natančnosti tekmečeve puške Dragunov izstreli puško z dolgimi prekinitvami.

Poglejmo še enkrat formulo. Kot lahko vidite, je frekvenca odvisna tudi od mase cevi. Masa debla je konstantna. Toda trden stik s čelo prinaša nepredvidljive pozitivne povratne informacije o cevi. Sistem-cev-sprednja roka (podpora) bo imel drugačen vztrajnostni moment (niz mas glede na točko pritrditve), kar pomeni, da lahko to povzroči tudi fazni premik. Zato športniki uporabljajo mehko podporo. Ista značilnost je povezana z uporabo načela "viseče cevi", ko čelo orožja nima trdega stika s cevjo in je nanj (orožje) trdno pritrjeno le v območju sprejemnik, drugi konec pa se sploh ne dotika cevi ali pa se dotika skozi vzmetni spoj (SVD).
Končna misel. Dejstvo, da z enako dolžino cevi ni mogoče doseči enake natančnosti pri različnih temperaturah, je odličen razlog za raztezanje možganov. Spremeniti je treba le dolžino in / ali maso cevi, ko se temperatura cevi spremeni. Brez spreminjanja dolžine ali teže cevi. Z vidika humanistike je to paradoks. Z vidika tehnika je idealna naloga. Vse življenje oblikovalca je povezano z reševanjem tovrstnih težav. Šerloki počivajo.






